VB(2)-苯

轨道/输入/输出文件下载

VB理论

可以参考 XMVB手册 A Chemist’s Guide to Valence Bond Theory

VB理论中术语与MO有对应关系

VBSCF$\to$MCSCF
VB结构$\to$自旋匹配组态
VB行列式$\to$行列式

MO中CI能量通过对角化CI矩阵得到。VBSCF能量也需要对角化VB行列式/VB结构为基的CI矩阵，由于VB结构之间不正交，需要求解:
$$HC = SCE$$
这和MO中非正交AO基Hartree-Fock的情况一致

为了消掉重叠矩阵$S$，一般使用对称正交化，正交化过程这里不过多赘述，可以参考Szabo Modern Quantum Chemistry:
总之我们需要找出一个矩阵$X$使得$X^\dagger S X = I$，在对称正交化中
$$X = S^{-1/2} = Us^{-1/2}U^\dagger$$
然后将$H$变换:
$$H’ = X^\dagger HX$$
最后求解
$$H’C’ = C’E$$
对角化后得到能量矩阵$E$，原系数矩阵$C=XC’$
$C’$为正交矩阵，满足$C^\dagger C = I$
$C$满足$C^\dagger S C = I$

实际计算中不需要求出所有态的系数和能量

MO理论中计算分子轨道成分时由于基函数不正交，有多种计算AO占比的方法

在VB理论中VB结构不正交，结构权重也有多种划分方法，最常见的是$\rm Coulson \space Chirgwin \space Weight$
$$W_K = \sum_L C_K S_{KL} C_L$$
这和MO中的$\rm Mulliken$划分方法一致

VB结构

理想情况下如果有2n个活性轨道，2n个活性电子，可以画出$\sum_{k=0}^{n} C_k^{2n}C_k^{2n-k}(2n-1-2k)!!$种VB结构

但是能画出的VB结构的数量比自旋匹配组态的数量(CAS(m,n)的CSF数量为$\frac{n!(n+1)!}{(\frac{1}{2}m)!(\frac{1}{2}m+1)!(n-\frac{1}{2}m)!(n-\frac{1}{2}m+1)! } $)还要多，导致线性相关

为了找全所有线性无关的VB结构，需要使用Rumer规则:

将所有轨道(任意顺序)排列在一圆上，只取连线不相交的结构

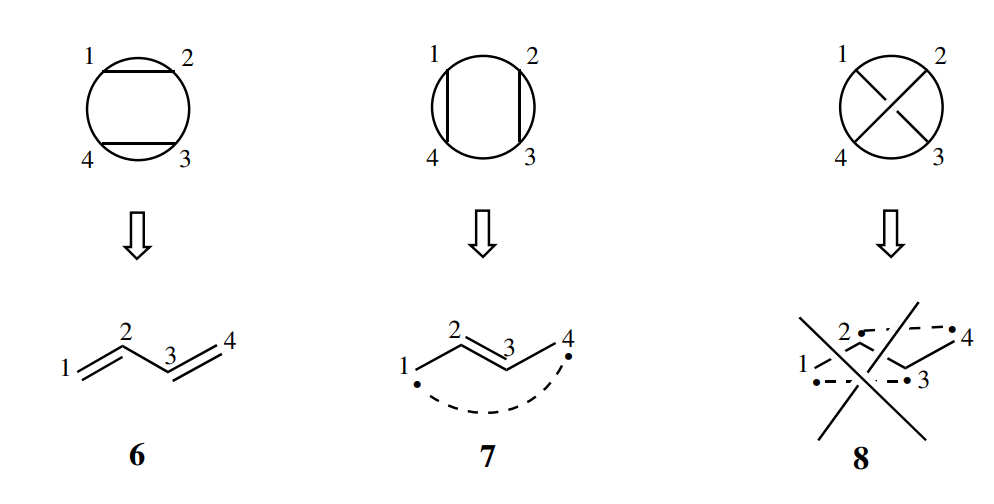
苯

这里结构和基组与官网上的例子完全相同，方便对比

C6H6
$ctrl
str=FULL nao=6 nae=6 iscf=5 iprint=3
orbtyp=hao frgtyp=sao
int=libcint basis=cc-pvdz
$end
$frag
12 2*6
spxpydxxdyydzzdxy 1-12
pzdxzdyz 1 2
pzdxzdyz 3 4
pzdxzdyz 5 6
pzdxzdyz 7 8
pzdxzdyz 9 10
pzdxzdyz 11 12
$end
$orb
1*18 1*6
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
2
3
4
5
6
7
$end
$geo
 C           0.6995000584   1.2115696411   0.0000000000
 H           1.2460106991   2.1581538376   0.0000000000
 C          -0.6995000584   1.2115696411   0.0000000000
 H          -1.2460106991   2.1581538376   0.0000000000
 C          -1.3990001169   0.0000000000   0.0000000000
 H          -2.4920213982   0.0000000000   0.0000000000
 C          -0.6995000584  -1.2115696411   0.0000000000
 H          -1.2460106991  -2.1581538376   0.0000000000
 C           0.6995000584  -1.2115696411   0.0000000000
 H           1.2460106991  -2.1581538376   0.0000000000
 C           1.3990001169   0.0000000000   0.0000000000
 H           2.4920213982   0.0000000000   0.0000000000
$end

str=full表示自动生成所有VB结构，此时不需要nstr=关键词和$str部分

计算苯时我们只使用6个pz轨道和6个π电子，nao=6 nae=6
VB结构共175个

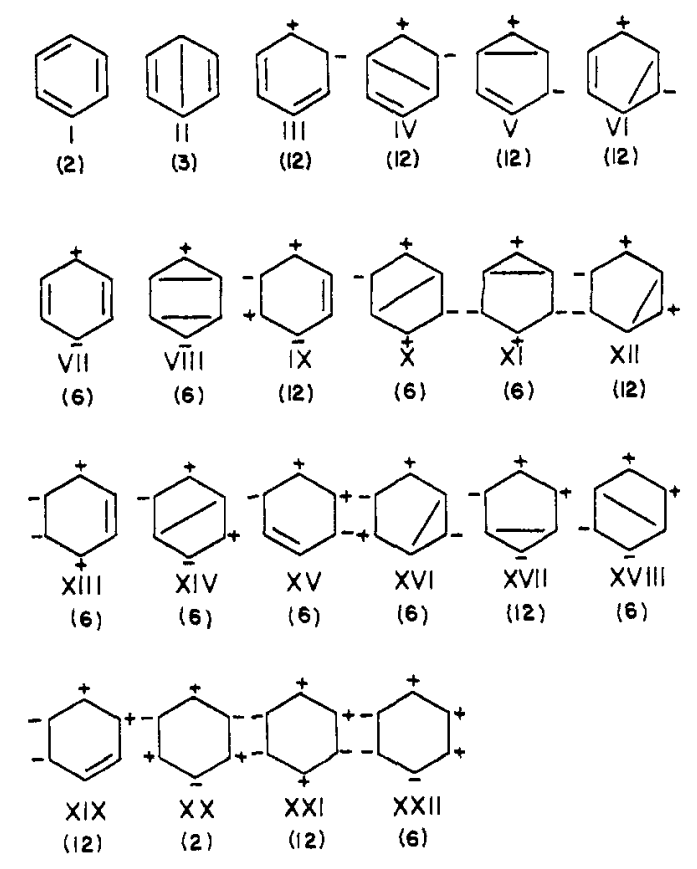
该图取自文献Valence-bond calculation of the electronic structure of benzene

$frag中2*6为C的pz轨道，其中包含了d极化函数，添加了与C相邻的H，使得轨道中可以混入部分H的pz极化函数
一个轨道分配一个片段，添加到$orb末尾(2,3,4,5,6,7)，这最后的6个轨道将作为6个活性轨道

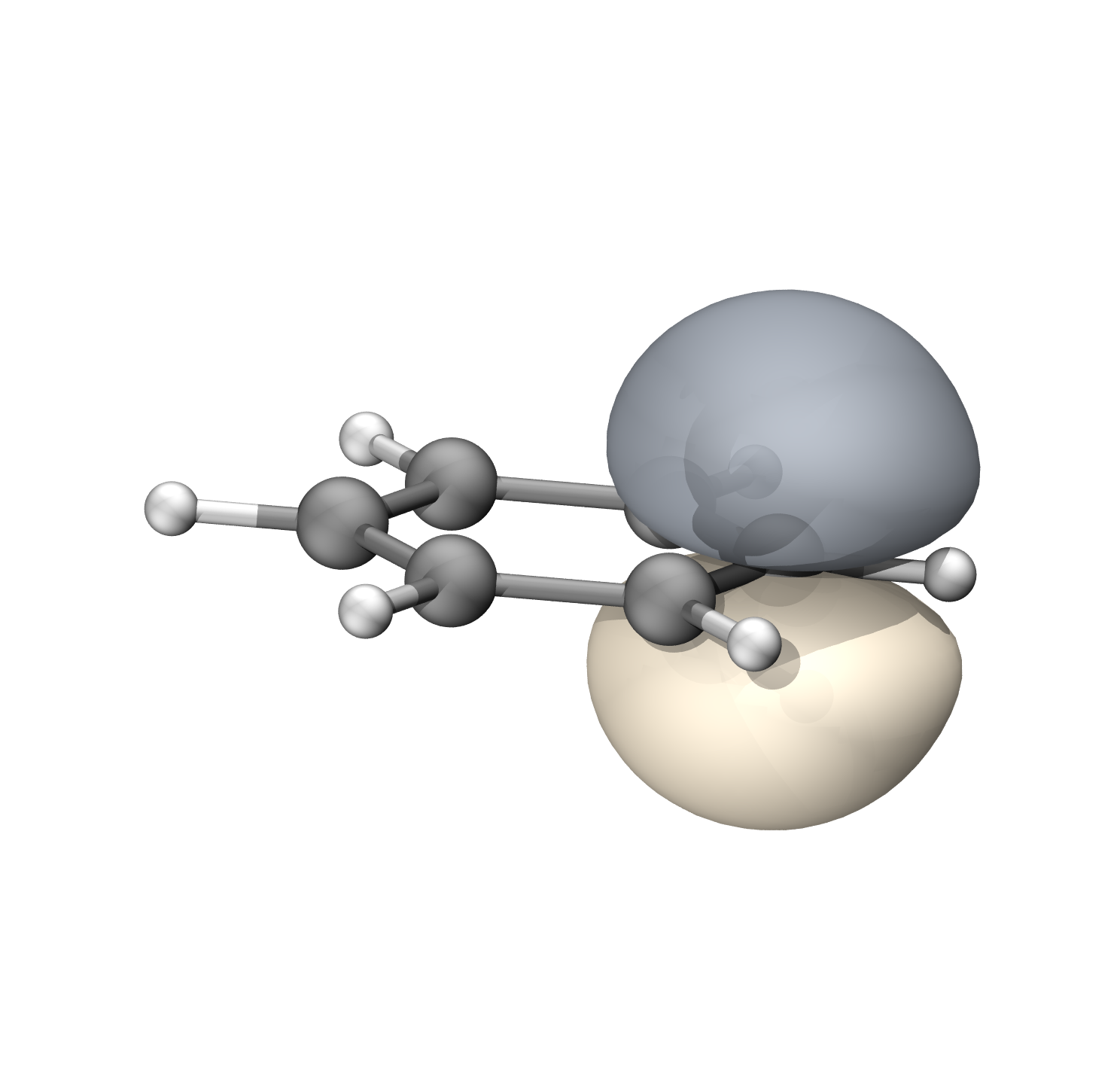
非活性轨道部分为双占据，包含σ部分和C的1s电子，为了简便以及能量最低，使用离域轨道
$frag中定义了一个包含所有原子，除去pzdxzdyz外所有基函数的片段12。并且在$orb中添加了18个包含该片段的轨道，guess=auto将会给出离域分子轨道，填充36个电子，剩余6个π电子作为活性电子

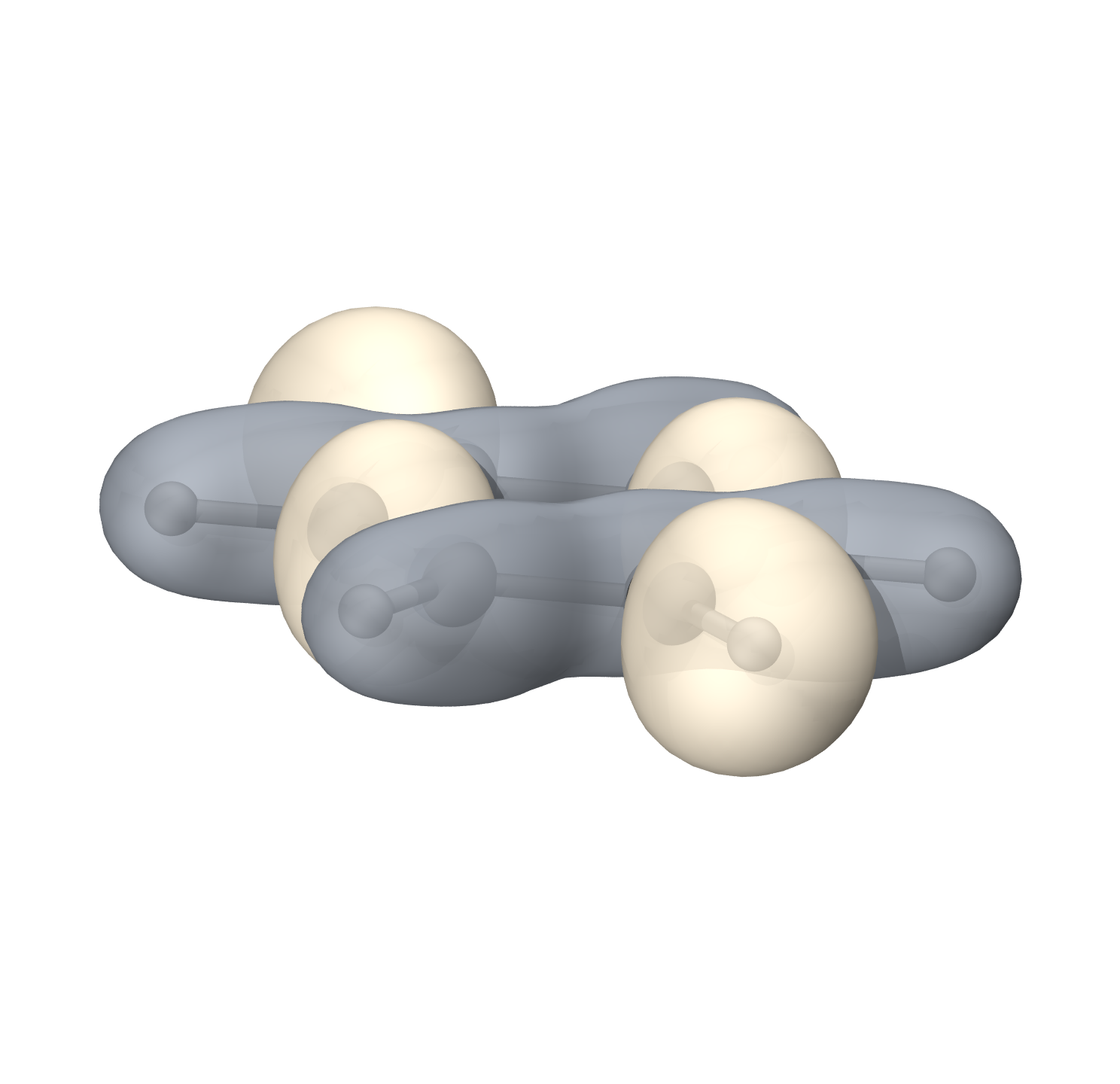离域轨道其中之一

仅两种共价结构

将str=full删除，添加nstr=2，在$str中定义共价结构

C6H6
$ctrl
nstr=2 nao=6 nae=6 iscf=5 iprint=3
orbtyp=hao frgtyp=sao
int=libcint basis=cc-pvdz
$end
$frag
12 2*6
spxpydxxdyydzzdxy 1-12
pzdxzdyz 1 2
pzdxzdyz 3 4
pzdxzdyz 5 6
pzdxzdyz 7 8
pzdxzdyz 9 10
pzdxzdyz 11 12
$end
$orb
1*18 1*6
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
2
3
4
5
6
7
$end
$str
1:18 19 20 21 22 23 24
1:18 24 19 20 21 22 23
%end
$geo
 C           0.6995000584   1.2115696411   0.0000000000
 H           1.2460106991   2.1581538376   0.0000000000
 C          -0.6995000584   1.2115696411   0.0000000000
 H          -1.2460106991   2.1581538376   0.0000000000
 C          -1.3990001169   0.0000000000   0.0000000000
 H          -2.4920213982   0.0000000000   0.0000000000
 C          -0.6995000584  -1.2115696411   0.0000000000
 H          -1.2460106991  -2.1581538376   0.0000000000
 C           0.6995000584  -1.2115696411   0.0000000000
 H           1.2460106991  -2.1581538376   0.0000000000
 C           1.3990001169   0.0000000000   0.0000000000
 H           2.4920213982   0.0000000000   0.0000000000
$end

str中两种结构写为:

1:18 19 20 21 22 23 24
1:18 24 19 20 21 22 23

前18个轨道为离域的双占据轨道，19-24为pz轨道

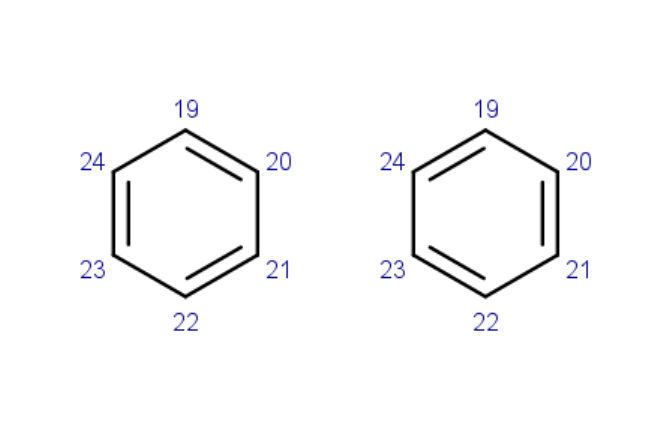
5种共价结构

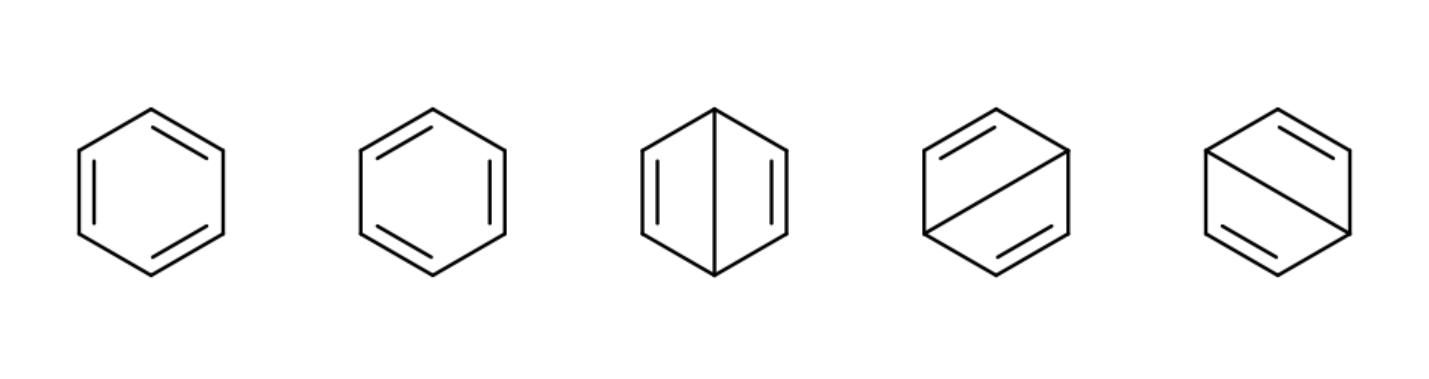
将str=full改为str=cov即可自动生成所有共价结构

str=ion(n,m)可以自动生成所有n阶和m阶离子结构(0阶离子结构为共价结构)
str=ion(n-m)生成所有n阶到m阶离子结构
例如str=ion(0,2,4-6)生成所有0阶、2阶、4阶到6阶离子结构

结果

能量:

结构	能量(Hartree)
1共价结构	-230.59097
2共价结构	-230.62995
5共价结构	-230.63449
full	-230.77728

相对于1共价结构的能量:

结构	能量(kcal/mol)
1共价结构	0
2共价结构	-24.45995
5共价结构	-27.30880
full	-116.90952

str=full时结构占比:

结构	Coulson Chirgwin Weight
共价结构I×2	21.91%
共价结构II×3	10.78%
1阶离子结构III*12	24.68%

结构	Renormalized Weight
共价结构I×2	39.83%
共价结构II×3	7.57%
1阶离子结构III*12	25.69%

可以看出离子结构是非常重要的MO中50%的离子项

对比一下CASSCF结果:
CASSCF(6,6)能量: -230.79382

结构	占比
222000	88.46%
211110	03.18%
220200	02.18%
202020	02.18%
121101	01.29%
112011	01.29%

占据数:

A2u	E1g	E1g	E2u	E2u	B2g
1.9604	1.9004	1.9004	0.1009	0.1009	0.0369

将6个π轨道定域化再进行CASSCF可以得到相同的能量

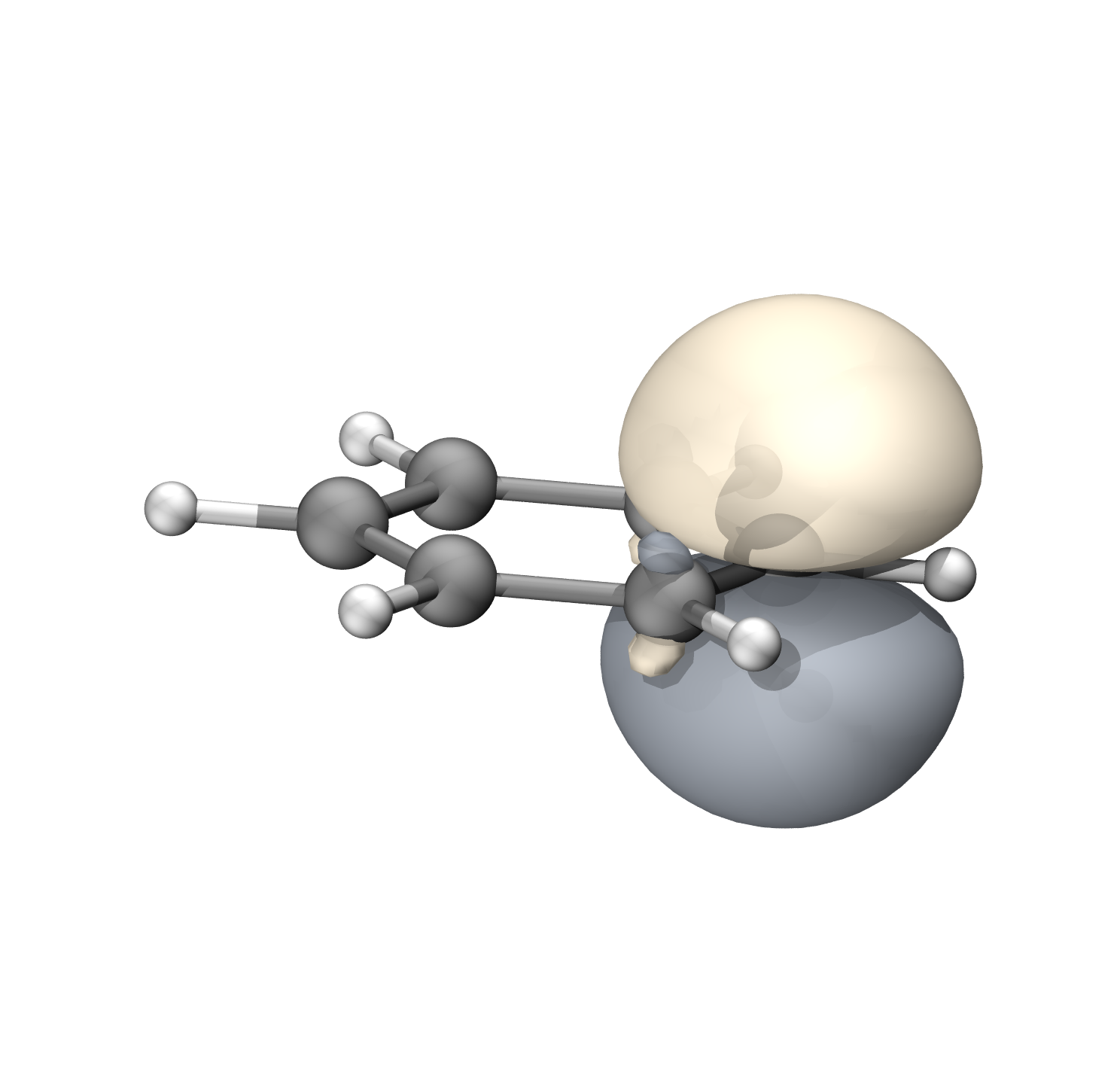
结构	占比
111111	23.98%
1111+2+0 ×12	37.32%

111111对应5个CSF
1111+2+0对应2个CSF

使用软件:
可视化轨道: VMD vcube
CASSCF计算: ORCA 6
VB计算: XMVB
转换XMVB轨道文件 XMVB-tools
计算轨道cube文件: Multiwfn