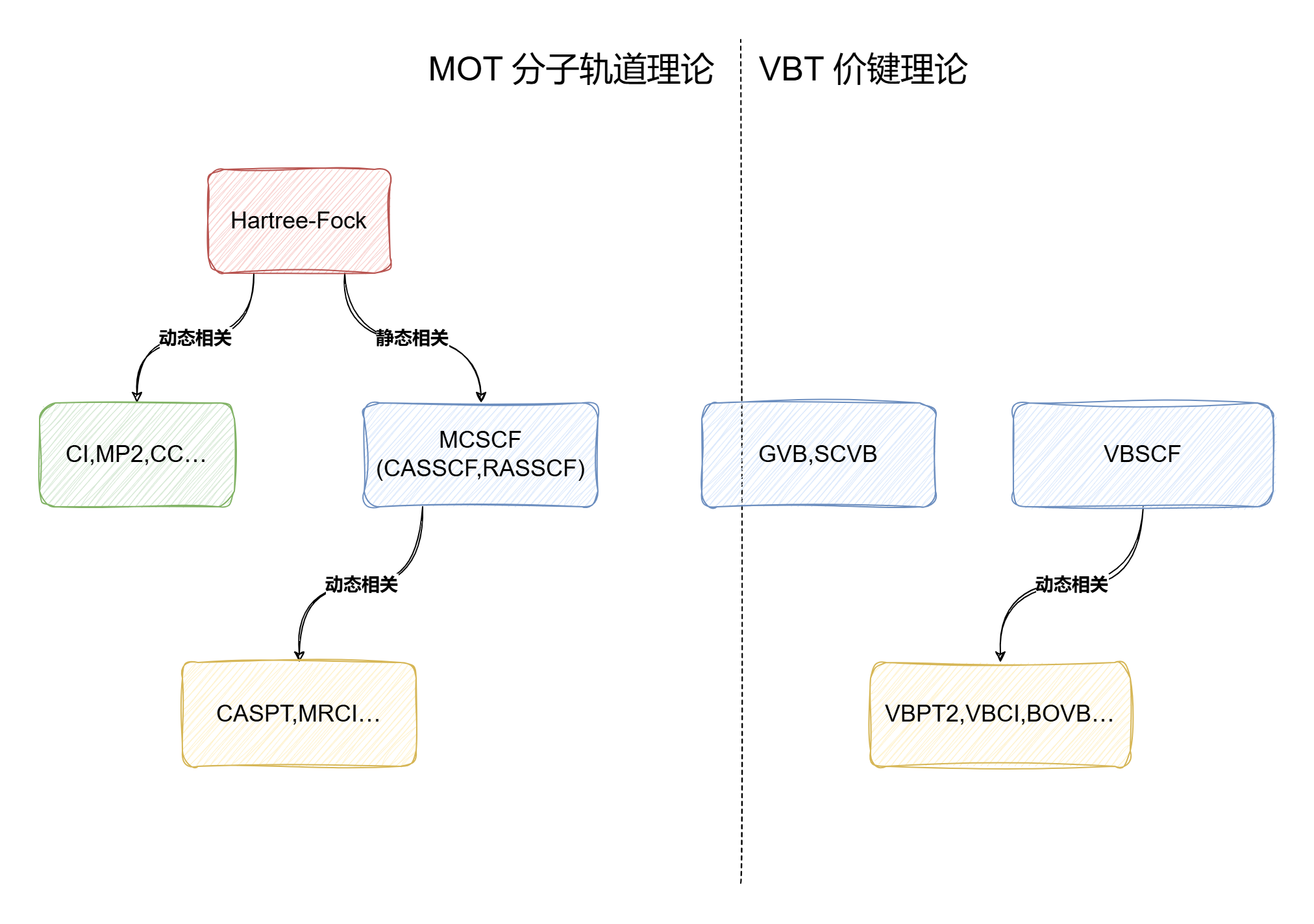
从头算VB方法分为两类，一类是基于严格定域轨道的VBSCF
另一类方法是基于Coulson-Fischer理论发展出的基于准离域轨道的广义价键(GVB)，以及自旋耦合价键(SCVB)。本文不涉及此类方法
XMVB中使用的VBSCF方法是一种多参考方法，相当于MO的MCSCF
该方法对于轨道没有特定要求（可以是离域/定域，正交/非正交），一般使用严格定域的轨道进行计算
氢分子
对于H2，VB理论使用严格定域的轨道，只包含共价结构
Coulson-Fischer理论只使用共价结构，但是允许轨道向另一个原子离域，这相当于间接引入了离子项
MO则使用完全离域的轨道，共价离子比例为1:1
在成键距离上，VB完全忽略了离子项，MO离子项过多，CF通过调整可以获得最佳的共价离子比例
在H2解离时，VB描述正确，CF的将逐渐减小为0，最后只剩共价项
而MO无论距离多远都具有一半的离子项，能量比实际更高，在越过Coulson-Fischer点后波函数将具有RHF->UHF不稳定性
对于VB，改进办法是引入离子结构
对于MO，需要引入组态相互作用(CI)，波函数将表示为基态组态+双激发到反键轨道的激发组态，解离时将趋于，最后只剩共价项
改进后的VB，MO和都可以自由调整共价离子比例，其结果相同(极小基下)
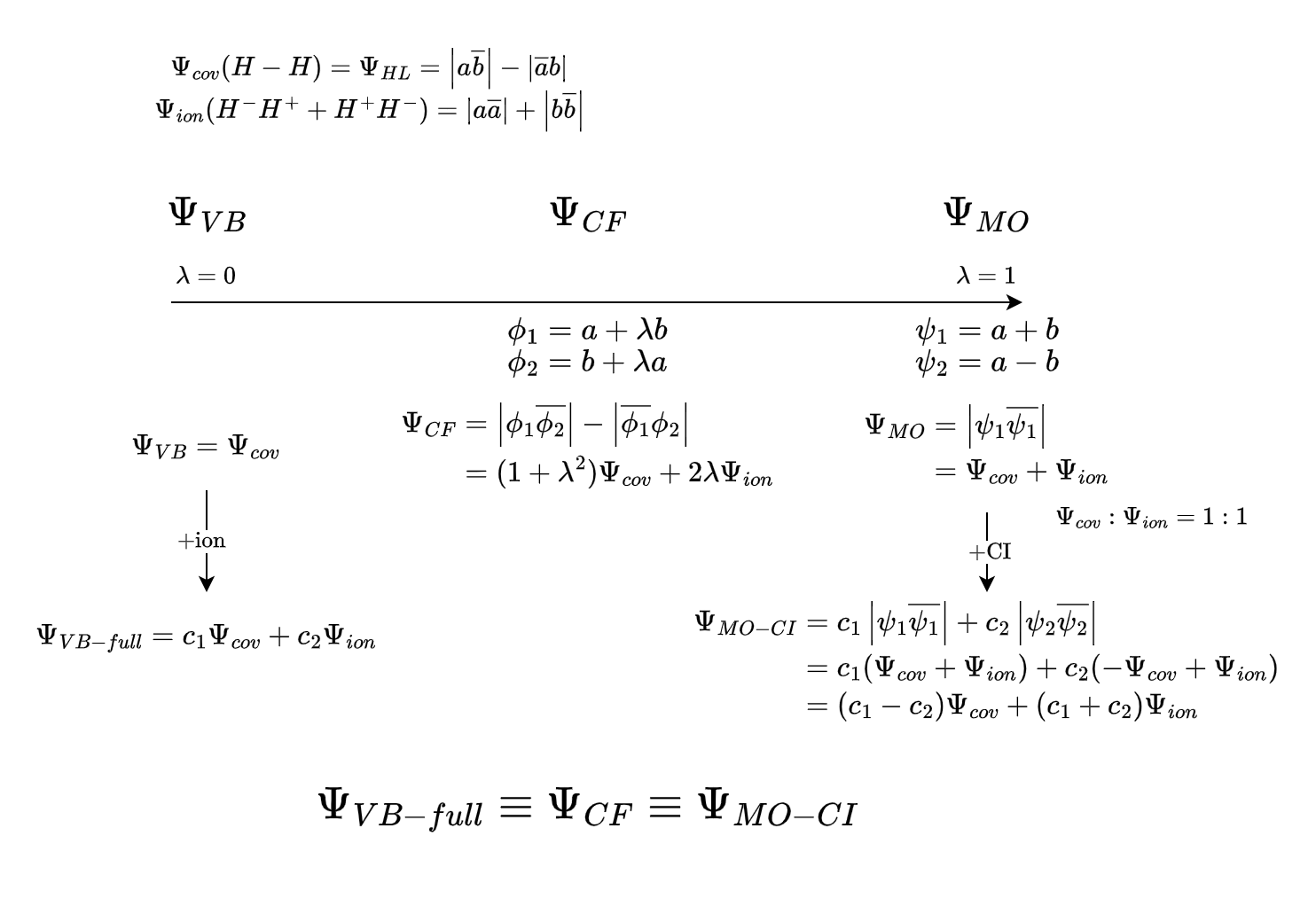*省略归一化系数
VB计算
输入文件：
H2
$ctrl
nstr=3 nao=2 nae=2 iscf=5 iprint=3
orbtyp=hao frgtyp=sao
int=libcint basis=def2-TZVP
$end
$frag
1*2 #两个片段，每个片段中包含一个原子
SPXPYPZDXXDYYDZZDXYDXZDYZ 1 #片段中包含原子1的s,p,d基函数
SPXPYPZDXXDYYDZZDXYDXZDYZ 2 #片段中包含原子2的s,p,d基函数
$end
$orb
1*2 #两个轨道，每个轨道中包含一个片段
1 #第一个轨道包含片段1
2 #第二个轨道包含片段2
$end
$str
1 1 #轨道1,1 离子结构H-H+
2 2 #轨道2,2 离子结构H+H-
1 2 #轨道1,2 共价结构H-H
$end
$geo #定义几何结构，单位为Å
H 0 0 0
H 0 0 0.75
$endnstr=3: 表示使用3个VB结构，结构将在$str中定义
nao=2 nae=2: 表示活性空间中使用2活性轨道，2活性电子
iscf: 指定轨道优化方法，手册中认为iscf=5是目前最有效的方法，iscf=5时需要定义nao和nae
iprint=3: 控制打印级别，最高级别为3
orbtyp: 指定VB轨道类型，HAO为杂化原子轨道，hao类型需要定义片段$frag
frgtyp: 默认值为atom这里使用frgtyp=SAO
int=libcint: 使用libcint计算积分
basis=def2-TZVP: 指定基组: def2-TZVP
未定义，使用默认值的选项:
vbftyp=det: 使用行列式
guess=auto: 默认初猜方法
ncharge=0 nmul=1: 电荷与自旋多重度
VBSCF: 如果没有指定计算方法，默认使用VBSCF
frag
$frag中第一行指定每个片段中有多少个原子，例如
8 2 2 2 2表示第一个片段中包含8原子，第2,3,4,5片段包含2原子，可以简写
8 2*4其余行每行定义一个片段
frgtyp=sao时需要指明片段中包含的基函数类型和原子
frgtyp=atom时需要指明片段中包含的原子
片段中定义多个连续的原子时1 2 3可以简写为1-3，例如
$frag
8 2*4
spxpydxxdyydzzdxy 1-8
pzdxzdyz 1 5
pzdxzdyz 2 6
pzdxzdyz 3 7
pzdxzdyz 4 8
$endorb
$orb中第一行指定每个轨道中有多少个片段，如果指定为0，则对应的轨道不会被优化
可以使用$frag中相同的方法简写
其余行每行定义一个轨道包含哪些片段
str
$str中定义VB结构，一行一个
VB结构中每两个轨道为一组，单电子写在最后面
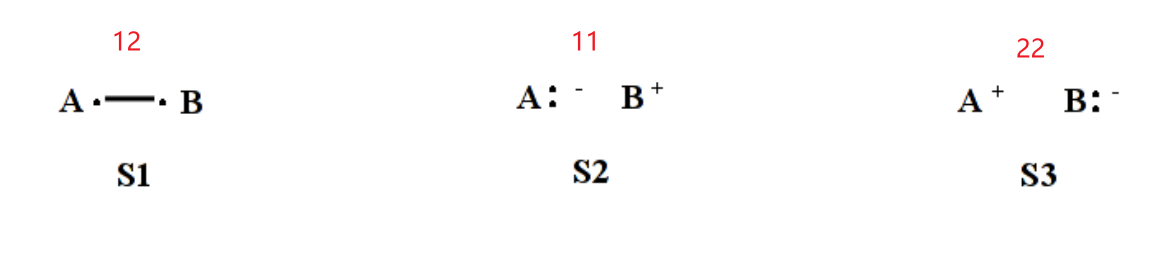两个轨道不同时为共价结构(即构成的自旋匹配组态)，相同时为离子结构()
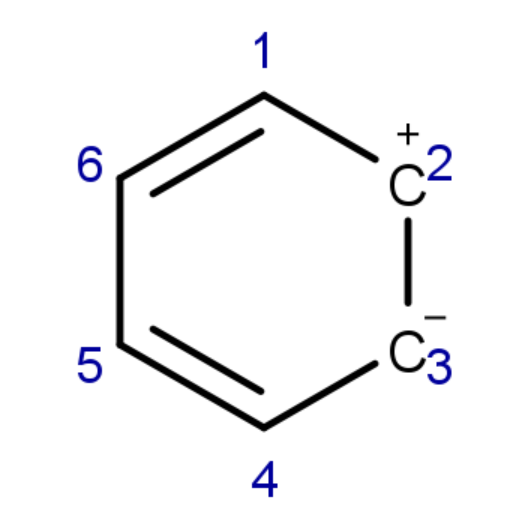
以该结构为例(仅考虑π电子)，VB结构写为:
1 6 5 4 3 3非活性轨道将保持双占据，(此时这些轨道例如: 1 1 2 2 3 3可以简写为1:3)
对于多个连续的共价结构例如:
1:18 19 20 21 22 23 24可以简写为:
1:18 19-24CF计算
在$ctrl中添加guess=read读取VB计算的轨道
将.orb文件中的内容复制到$gus中，或复制该文件并将后缀改为.gus
修改$frag让片段中包含两个原子，使轨道可以向另一原子离域
nstr改为1，$str中只使用共价结构
$ctrl
nstr=1 nao=2 nae=2 iscf=5 iprint=3
orbtyp=hao frgtyp=sao
int=libcint basis=def2-TZVP
guess=read
$end
$frag
2*2
SPXPYPZDXXDYYDZZDXYDXZDYZ 1 2
SPXPYPZDXXDYYDZZDXYDXZDYZ 2 1
$end
$orb
1*2
1
2
$end
$str
1 2
$end
$gus
4 4
# ORBITAL 1 NAO = 4
0.3280788041 1 0.5473780520 2 0.2483494402 3 0.0465649707 6
# ORBITAL 2 NAO = 4
0.3280788041 7 0.5473780520 8 0.2483494402 9 -0.0465649707 12
$end
$geo
H 0 0 0
H 0 0 0.75
$endCASSCF计算
修改$frag使片段中包含两个原子，此时guess=auto将给出完全离域的轨道
$ctrl
nstr=3 nao=2 nae=2 iscf=5 iprint=3
orbtyp=hao frgtyp=sao
int=libcint basis=def2-TZVP
$end
$frag
2
SPXPYPZDXXDYYDZZDXYDXZDYZ 1 2
$end
$orb
1*2
1
1
$end
$str
1 1
2 2
1 2
$end
$geo
H 0 0 0
H 0 0 0.75
$end最后CF与MO给出的能量均为-1.1511，VB能量稍微高，为-1.1506(极小基下相同)
三者轨道
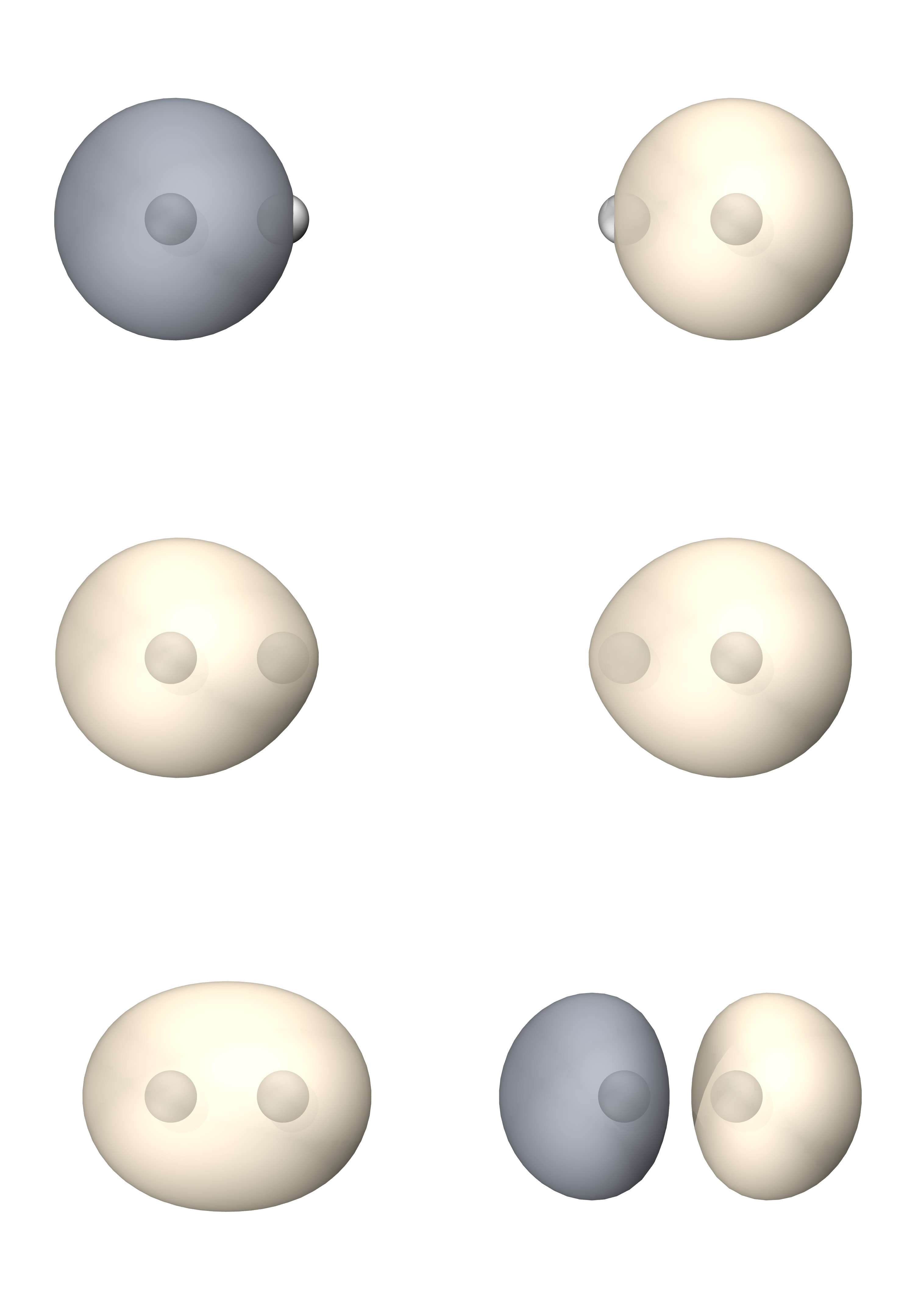
VBCI,MRCI
将iscf更改为1,添加guess=read读取之前计算的轨道，添加VBCISD请求CI计算
$ctrl
nstr=3 nao=2 nae=2 iscf=1 iprint=3
orbtyp=hao frgtyp=sao VBCISD
int=libcint basis=def2-TZVP
guess=read
$end
$frag
1*2
SPXPYPZDXXDYYDZZDXYDXZDYZ 1
SPXPYPZDXXDYYDZZDXYDXZDYZ 2
$end
$orb
1*2
1
2
$end
$str
1 1
2 2
1 2
%end
$gus
6 6
# ORBITAL 1 NAO = 6
0.3464429020 1 0.5433704588 2 0.2352323485 3 -0.0000000000 4
0.0000000000 5 0.0325352138 6
# ORBITAL 2 NAO = 6
0.3464429020 7 0.5433704588 8 0.2352323485 9 -0.0000000000 10
0.0000000000 11 -0.0325352138 12
$end
$geo
H 0 0 0
H 0 0 0.75
$end对于MO也一样，读取CASSCF轨道
$ctrl
nstr=3 nao=2 nae=2 iscf=1 iprint=3
orbtyp=hao frgtyp=sao VBCISD
int=libcint basis=def2-TZVP
guess=read
$end
$frag
2
SPXPYPZDXXDYYDZZDXYDXZDYZ 1 2
$end
$orb
1*2
1
1
$end
$str
1 1
2 2
1 2
$end
$gus
12 12
# ORBITAL 1 NAO = 12
0.1882483830 1 0.2924576257 2 0.1290586913 3 0.0000113152 4
0.0000167536 5 0.0182022087 6 0.1883825923 7 0.2925821898 8
0.1290645452 9 -0.0000341486 10 0.0000212130 11 -0.0182519720 12
# ORBITAL 2 NAO = 12
-0.3954836105 1 -0.7729508582 2 -0.0521907282 3 0.0000000485 4
0.0000006432 5 0.0268703782 6 0.3954813178 7 0.7729522145 8
0.0521945576 9 0.0000000901 10 -0.0000004659 11 0.0268686017 12
$end
$geo
H 0 0 0
H 0 0 0.75
$end此时相当于FCI，二者给出的结果相同，能量均为-1.1682
BOVB
BOVB(Breathing Orbital Valence Bond)是一种VB特有的考虑动态相关的方法
VBSCF中所有VB结构使用同一套轨道，而在BOVB中每个VB结构都有一套独立的轨道，分别优化
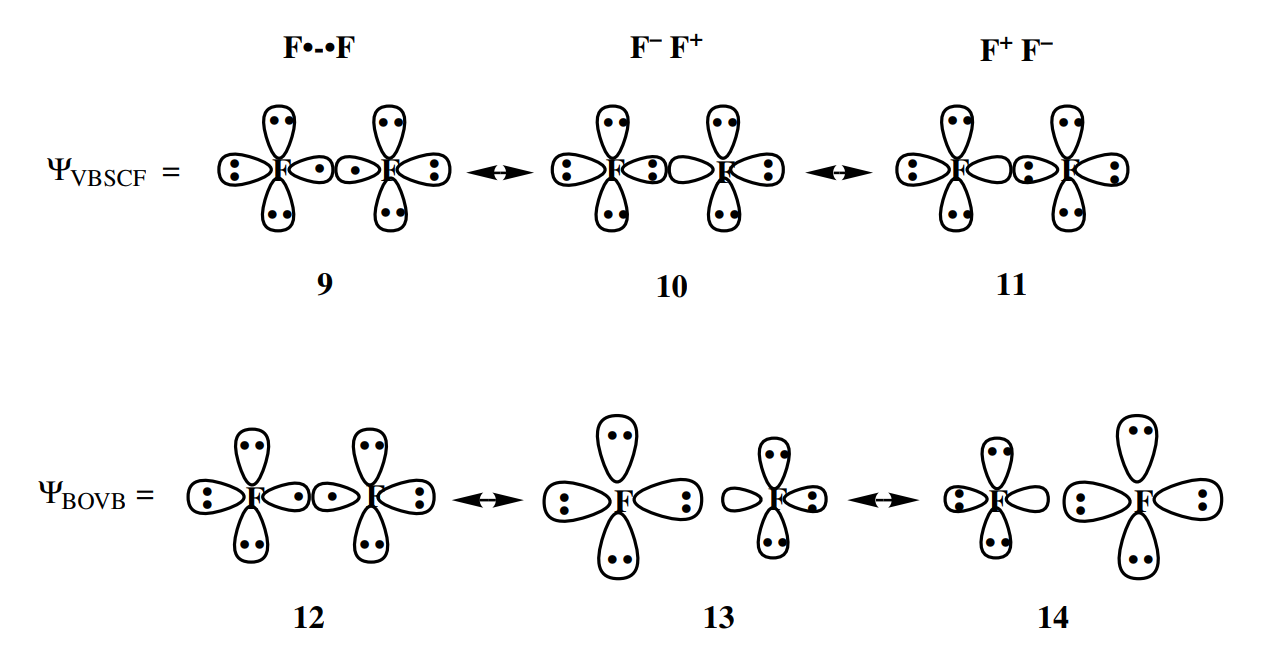
将iscf改为1，读取VB轨道，添加BOVB请求BOVB计算
$ctrl
nstr=3 nao=2 nae=2 iscf=1 iprint=3 BOVB
orbtyp=hao frgtyp=sao
int=libcint basis=def2-TZVP
guess=read
$end
$frag
1*2
SPXPYPZDXXDYYDZZDXYDXZDYZ 1
SPXPYPZDXXDYYDZZDXYDXZDYZ 2
$end
$orb
1*2
1
2
$end
$str
1 1
2 2
1 2
$end
$gus
6 6
# ORBITAL 1 NAO = 6
0.3464429020 1 0.5433704588 2 0.2352323485 3 -0.0000000000 4
0.0000000000 5 0.0325352138 6
# ORBITAL 2 NAO = 6
0.3464429020 7 0.5433704588 8 0.2352323485 9 -0.0000000000 10
0.0000000000 11 -0.0325352138 12
$end
$geo
H 0 0 0
H 0 0 0.75
$end一些有用的输入
ITMAX=n: 设置最大SCF迭代次数，默认为200
NSTATE=n: 计算n阶激发态，默认为0（基态）
SORT: 按照系数从大到小排列VB结构
OUTPUT=AIM: 输出记录自然轨道的.wfn文件
DEN: 输出密度矩阵到.den文件
VB计算你可能会遇到
基组稍大就很难收敛活性空间大一些就算不动算起来极慢极其消耗内存
使用软件:
可视化轨道: VMD vcube
CASSCF计算: ORCA 6
VB计算: XMVB
转换XMVB轨道文件 XMVB-tools
计算轨道cube文件: Multiwfn
参考文献: